Continuous Maps of the Unit Circle Iknto the Plane
This short article on a type of circle is quite straightforward but it has very important applications to the mathematical field of trigonometry. Before we start though, we should ask, what is a circle?
What is a circle?
A circle is a very important shape (a shape is sometimes called a locus) that consists of all points in a plane, which are at a given distance called the radius from a particular point called the centre. The length of a circle is called its circumference.
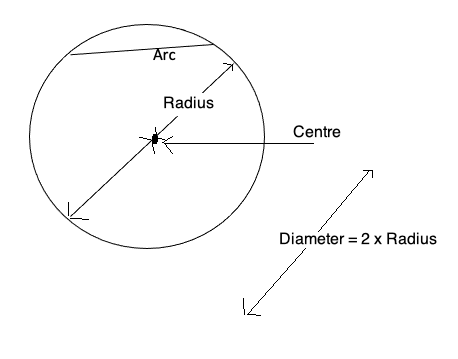
The diagram below shows a circle. No matter what point you choose on the circle, the shortest distance to the centre is the radius, which always has the same length. The longer line is twice the radius and is called the diameter.
Shorter, straight lines, which don't go through the centre, connecting different parts of the circle are called arcs.
Circles in a Cartesian plane
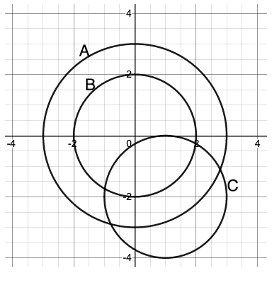
The diagram above shows 3 circles in a coordinate or Cartesian plane. A is centred at (0,0) and has a radius of 3. B is centred at (0,0) and has a radius of 2. C is centred at (1,-2) and has a radius of 2.
The Unit Circle
The unit circle is a circle in the Cartesian plane centred at (0,0), often called the origin, with radius 1.
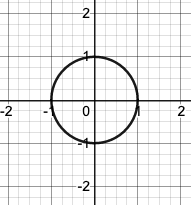
The diagram above shows a unit circle.
Why is the unit circle so important?
The unit circle gives an easy method of defining the sine and cosine functions that you have probably met before, since for an arbitrary angle (see diagram below), the radius making an angle with the x-axis cuts the unit circle at the point whose x-coordinate is cos and whose y-coordinate is sin .
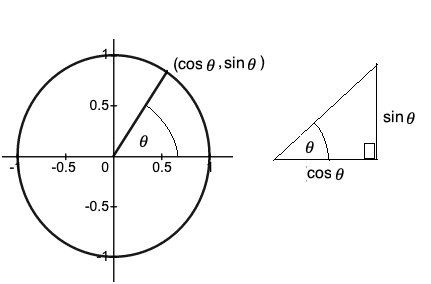
This is really useful because using this method of defining the sine and cosine functions, we can easily find the sine and cosine of such angles as 120o, 223o, and 310o, which was impossible with the right-angled triangles of early math courses, where trigonometry is introduced, in high school.
The diagrams below show how this can be done.
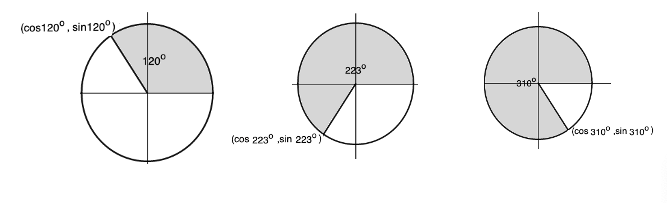
Note that the angles are positive and go anti-clockwise.
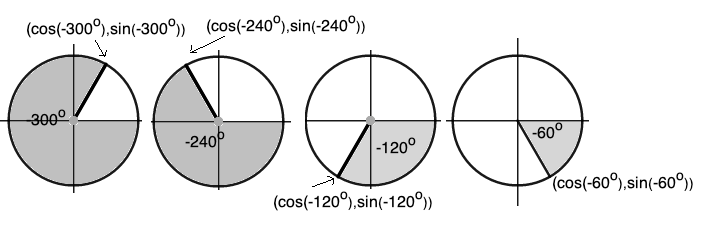
We can have negative angles, but they go clockwise. See the diagram below.
Early Trigonometry: Pythagoras and SOHCAHTOA
We mentioned before that in early math courses, where trigonometry is introduced in high school, students are taught about Pythagoras' Theorem and using the trigonometric functions to find sides and angles of right-angled triangles in both theoretical and practical situations. It is impossible to meaningfully get the trigonometric functions in such situations of angles greater than 90o or less than 0o.
Calculators
An examination of any scientific calculator will show that sines and cosines can be worked out very easily using these devices. This is a skill that you probably have already, so we won't dwell on it in this article. With calculators, it is easy to get the trigonometric functions of angles greater than 90o or less than 0o.
There is another function that is important in trigonometry and this is the tangent function. As you are probably well aware, this function is also on scientific calculators.
Is tangent easily seen on the unit circle?
We will try to answer this in the next paragraph.
The tangent function and the unit circle
Does the unit circle provide an easy way of getting tangents, in the same way, that it does for sine and cosine? The answer is yes. The diagram below shows this.
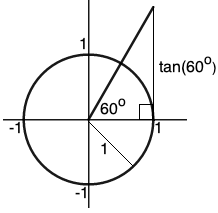
It is actually easier to see on a diagram than it is to say by words. If you wanted to describe it then you could say that it is the distance of the point of intersection of the angle line and the line perpendicular to the x-axis from the x-axis, which is of distance 1 from the origin!
Another thing that you may have noticed on calculators is that you can measure angles in different ways. The way that you are probably familiar with is using degrees. There are other ways of measuring angles, one, and this is also found on nearly all scientific calculators, are radians. Radians are so important that apart from mentioning them here, they will be left for a separate article.
All scientific calculators can switch between degrees, radians, and, in some cases, other ways of measuring angles.
Angles greater than 360o
Having noticed that on calculators you can have angles of any size, you may wonder how the unit circle can also do this. This is easily explained using the unit circle definitions of the trigonometric functions. The trigonometrical functions, sine, and cosine are often called circular functions. The reason for this is that they are defined by finding the coordinates of points on a unit circle. Angles, which are greater than 360° are treated as though they were the angle obtained as a remainder after the large angle is divided by 360.
Example
What angle, which lies between 0o and 360o, has the same cosine and sine as 779o?
Answer
779 = 2 360 + 59.
cos779o = cos59o and sin779o = sin59o.
What about signs?
You may have noticed that if you have angles that are larger than 90° then the cosine and the sine are sometimes negative. To calculate when these functions will be positive and when they will be negative, it is useful to divide the unit circle into four equal parts called quadrants. The diagram below shows these.
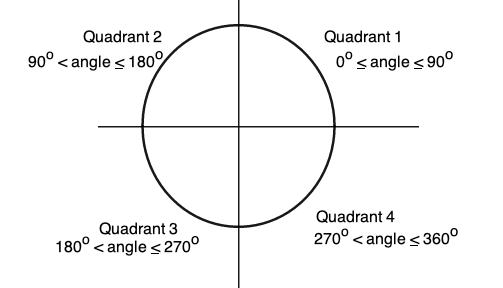
To determine in which quadrants circular functions are positive, the mnemonic All Science Teachers Cr y is very helpful. In this: A stands for All positive, S stands for Sine is positive, T stands for Tangent is positive and C stands for Cosine is positive. With this, circular functions of any angle can be used by using acute angles. Have a look at the diagram.
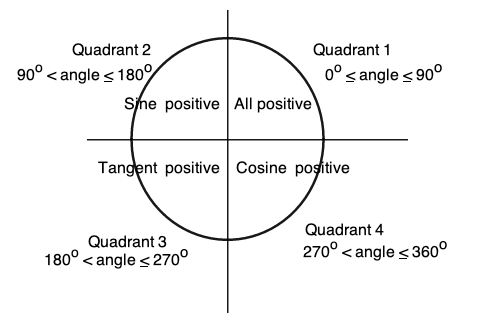
How does this work?
Example 1
Find the cosine, sine, and tangent of 120o .
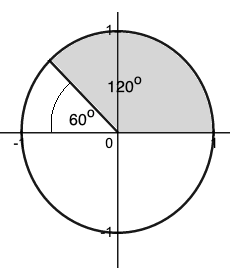
120o is a second quadrant angle.
In the second quadrant, the angle needs to be subtracted from 180o to get the acute angle, which will give the answers.
Hence, the acute angle is 180o – 120o = 60o.
sin120o = sin60o = 0.8660 (Only sine is positive in quadrant 2)
cos120o = -cos60o = -0.5 (Only sine is positive in quadrant 2)
tan120o = -tan60o = -1.732 (Only sine is positive in quadrant 2)
Example 2
Find the cosine, sine, and tangent of 240o
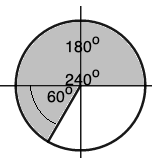
240o is a third quadrant angle.
In the third quadrant, 180o needs to be subtracted from the angle to get the acute angle, which will give the answers.
Hence, the acute angle is 240o – 180o = 60o.
sin240o = -sin60o = -0.8660 (Only tangent is positive in quadrant 3)
cos240o = -cos60o = -0.5 (Only tangent is positive in quadrant 3)
tan240o = tan60o = 1.732 (Only tangent is positive in quadrant 3)
Example 3
Find the cosine, sine, and tangent of 300o
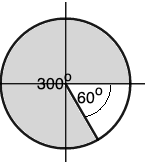
300o is a fourth quadrant angle.
In the fourth quadrant, the angle needs to be subtracted from 360o to get the acute angle, which will give the answers.
Hence, the acute angle is 360o – 300o = 60o.
sin300o = -sin60o = -0.8660 (Only cosine is positive in quadrant 4)
cos300o = cos60o = 0.5 (Only cosine is positive in quadrant 4)
tan300o = -tan60o = -1.732 (Only cosine is positive in quadrant 4)
What about negative angles?
If you have a negative angle, then all you need to know is which quadrant you're in.
A negative angle has the same values for circular functions as the negative angle added to 360o.
Example 4
The following example shows this.
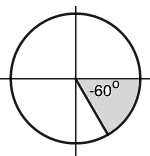
-60o is a fourth quadrant angle. We add -60o to 360o, which gives 300o.
In the fourth quadrant, the angle needs to be subtracted from 360o to get the acute angle, which will give the answers.
Hence, the acute angle is 360o – 300o = 60o.
sin(-60o) = sin300o = -sin60o = -0.8660 (Only cosine is positive in quadrant 4)
cos(-60o) = cos300o = cos60o = -0.5 (Only cosine is positive in quadrant 4)
sin(-60o) = tan300o = -tan60o = -1.732 (Only cosine is positive in quadrant 4)
Bounds for the sine and cosine functions
An examination of the unit circle shows that both cos (x) and sin (x) lie between -1 and 1.
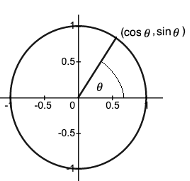
Hence, -1 < sin(x) < 1 and -1 < cos(x) < 1.
Two important Identities
Two other very important facts may be gleaned from the unit circle. Important facts, such as these, are often called identities.
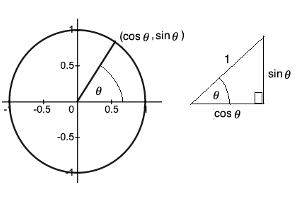
(i) From the little angle on the right, if Pythagoras' Theorem is applied, which states that, the square of the hypotenuse is equal to the sum of the squares of the other two sides.
We get the very important result that (sin)2 + (cos)2 = 12,
which is usually written as sin 2 + cos 2 = 1. This is a result that is of great importance.
(ii) Using high school trigonometry, tan = opposite/adjacent = sin/cos. This is also of great importance. It is how the tangents of angles may be found. All that is necessary is to divide the sine of the angle by the cosine. For this reason, any angle, such as 90o or 270o, where the cosine is 0, will not have a tangent.
Source: https://visualfractions.com/blog/the-unit-circle/
0 Response to "Continuous Maps of the Unit Circle Iknto the Plane"
Post a Comment